Jared Tarbell

Christopher Langton, one of the founders of artificial life, began his work by studying one-dimensional cellular automata. He thought of one of the states of an automaton as being “dead”. All the remaining states were thought of as “alive”. Langton only worked with automata with the property that if a cell and are its neighbors are dead, then that cell will remain dead in the next generation.

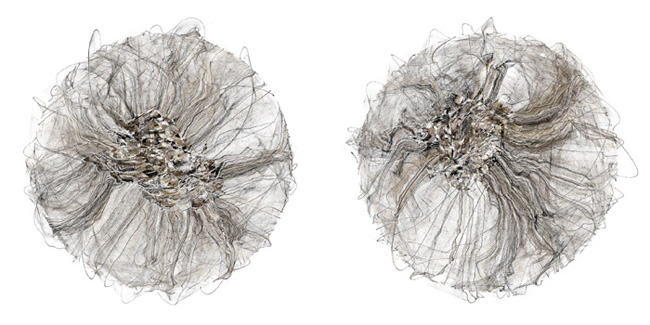
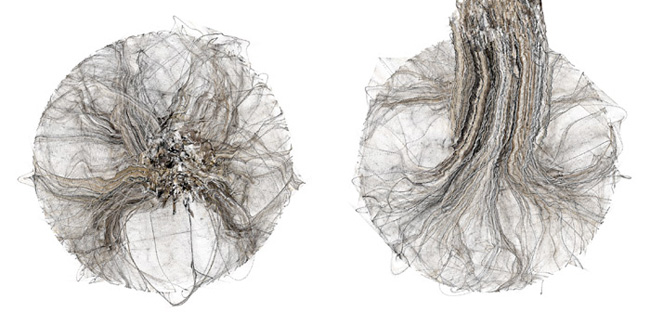
Some CA’s (Cellular Automata)… die out in a few generations or… quickly settle into simple repeating patterns. Langton said that these CA’s were highly “ordered”. Their behavior is… extremely predicatable and easy to describe. Other CA’s… seem to be random. Langton called such CA’s “chaotic”. Their behavior is… completely unpredictable, and can only be described as a mass of unrelated details. But some CA’s display interesting, complex, almost lifelike behavior. Langton said that these CA’s are near the border between order and chaos. If they were more ordered, they would be too predictable; if they were less ordered, they would be too chaotic.

Langton defined a simple number that can be used to help predict whether a given CA will fall in the ordered realm, in the chaotic realm, or near the boundary, on the “edge of chaos.” The number can be computed from the rules of the CA. It is simply the fraction of rules in which the new state of the cell is living. (The rule in which a cell and all its neigbors are dead is not counted, since Langton assumed that the new state in this rule is always death.) He called this parameter “lambda.”

The lambda parameter of a CA is a number between 0 and 1. If lambda is 0, then all cells die immediately, since every rule leads to death. If lambda is 1, then any cell that has at least one living neighbor will stay alive in the next generation and, in fact, forever. More generally, values of lambda close to zero give CA’s in the ordered realm. Values close to 1 give CA’s in the chaotic realm. The edge of chaos is somewhere in between.

Text sourced from “Edge of Chaos” by David Eck. To view more of Jared Tarbell’s amazing computational explorations, for lack of a better word, please visit Gallery of Complexification. Do take a look at the flash animations as well. They are truly fascinating.